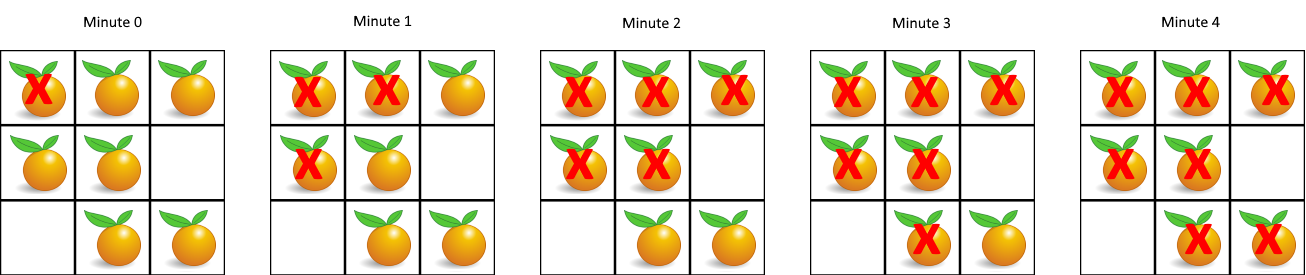
994. Rotting Oranges

You are given an m x n grid where each cell can have one of three values:

• 0 representing an empty cell,
• 1 representing a fresh orange, or
• 2 representing a rotten orange.

Every minute, any fresh orange that is 4-directionally adjacent to a rotten orange becomes rotten.

Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1.

class Solution:
    def orangesRotting(self, grid: List[List[int]]) -> int:
		"""
        we are trying to find the max distance
        between a fresh orange and any rotting orange
        
        count how many fresh oranges there are 
        (O(n)) where n is number of cells
        BFS from all the rotting oranges in parallel
            when we see a fresh orange, turn it rotten and decrement orange counter
                if fresh orange count goes to 0, return current time
            at each "layer", increment minute counter by 1
            if bfs ends and fresh oranges exist, return -1
		"""
            
        dirs = [[0,1],[1,0],[-1,0],[0,-1]]
            
        t = 0
        fresh = 0
        q = deque()
        
        # count fresh oranges
        # enqueue rotten oranges
        for i, row in enumerate(grid):
            for j, cell in enumerate(row):
                if cell == 1:
                    fresh += 1
                elif cell == 2:
                    q.append((i, j))
 
        while q:
            level_len = len(q)
            
            for _ in range(level_len):
                i, j = q.popleft()
                if grid[i][j] == 1:
                    fresh -= 1
                    grid[i][j] = 2 # make orange rotten if fresh
                
                if fresh == 0:
                    return t
                
                for d in dirs:
                    ni, nj = i + d[0], j + d[1]
                    if ni >= 0 and ni < len(grid) and nj >= 0 and nj < len(grid[0]):
                        if grid[ni][nj] == 1:
                            q.append((ni, nj))
            
            t += 1
        
        return -1 if fresh > 0 else t

• bfs from all rotten oranges at the same time in parallel.
• kind of similar idea to 542-01-matrix.

Related.

• 542-01-matrix.

Categories:: matrix, bfs