987. vertical order traversal of a binary tree

Given the root of a binary tree, calculate the vertical order traversal of the binary tree.

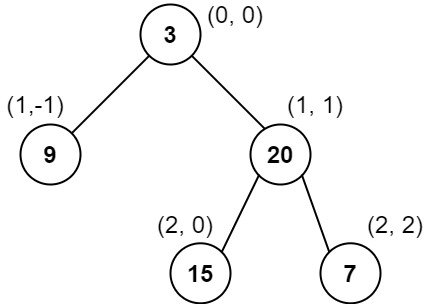
For each node at position (row, col), its left and right children will be at positions (row + 1, col - 1) and (row + 1, col + 1) respectively. The root of the tree is at (0, 0).

The vertical order traversal of a binary tree is a list of top-to-bottom orderings for each column index starting from the leftmost column and ending on the rightmost column. There may be multiple nodes in the same row and same column. In such a case, sort these nodes by their values.

Return the vertical order traversal of the binary tree.

solution

We do vertical order traversal, in a level-wise BFS. Then, we just sort the given levels columns and append to res.

def verticalTraversal(self, root: Optional[TreeNode]) -> List[List[int]]:
	if not root:
		return []
	  
	res = deque()
	left_bound = inf
	q = deque([(root, 0)])
	  
	while q:
		level_len = len(q)
		by_col = defaultdict(list)
 
		for _ in range(level_len):
			cur, col = q.popleft()
			if col < left_bound:
				left_bound = col
				res.appendleft([])
			elif col - left_bound >= len(res):
				res.append([])
 
			by_col[col].append(cur.val)
	  
			if cur.left:
				q.append((cur.left, col-1))
			if cur.right:
				q.append((cur.right, col+1))
 
		for col in by_col:
			res[col-left_bound].extend(sorted(by_col[col]))
 
	return res