84. largest rectangle in histogram

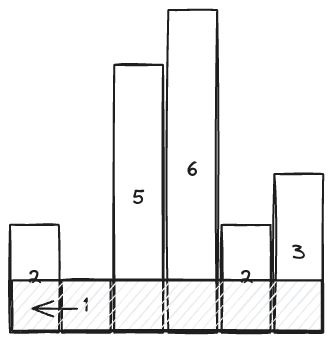
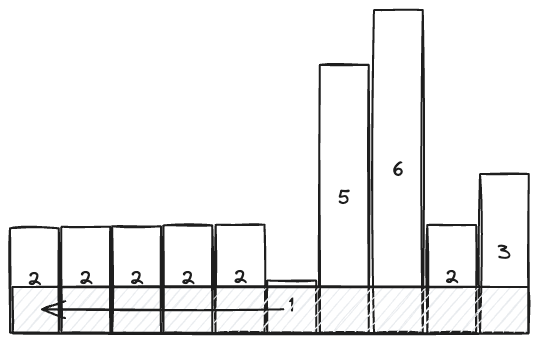
Given an array of integers heights representing the histogram’s bar height where the width of each bar is 1, return the area of the largest rectangle in the histogram.

solutions

divide and conquer

 def largestRectangleArea(self, heights: List[int]) -> int:
	  def calculateArea(heights: List[int], start: int, end: int) -> int:
			if start > end:
				 return 0
			min_index = start
			for i in range(start, end + 1):
				 if heights[min_index] > heights[i]:
					  min_index = i
			return max(
				 heights[min_index] * (end - start + 1),
				 calculateArea(heights, start, min_index - 1),
				 calculateArea(heights, min_index + 1, end),
			)
 
	  return calculateArea(heights, 0, len(heights) - 1)

monotonic stack

The intuition here is that the largest rectangle that we can make will be the height of the smallest bar that is included.

For example, this is the largest value rectangle that uses the second-last bar of height 2.

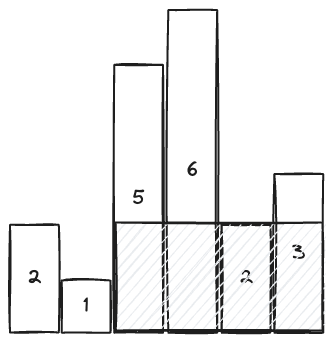
Note that we can’t extend the bar left anymore, as $1<2$ and would make the rectangle invalid.

So, we know that when using a bar of height $n$, the rectangle that uses it can only extend left until it meets a bar that is shorter. Without loss of generality, this applies to the right as well.

This gives us an intuition for how to solve this problem. We will try to find the largest rectangle that we can draw using each bar $b_i$. When we encounter a shorter bar as we iterate from left to right, we know that the previous bars that are taller must now end, and we calculate the area that we amassed.

A monotonic stack works for this, as we keep track of all the bars that are currently still “accumulating”.

Some things to consider

Unlike a standard monotonic stack question, we also need to store the index where the current bar’s rectangle starts.

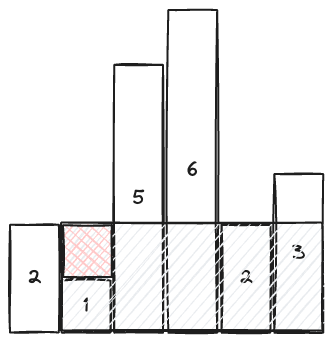
In a non-special case, such as the first rectangle, we know that the rectangle’s left bound is just it’s own index. However, consider the second bar in the diagram above. We can see that it’s index will actually extend to the left, including the first bar of height 2.

Thus, when we are ending the accumulation of prior taller bars, we need to keep track of how many we pop off, and extend the new shorter bar that we’re pushing onto the stack as far left as we popped off (as every prior bar we popped off the stack is taller than the current bar, and so the current bar’s rectangle can extend back through those bars).

This applies for any number of prior bars that need to be popped.

Finally, the other edge case to consider is when values remain on the stack after we reach the end of our array iteration. These rectangles have essentially accumulated all the way to the end of the bar graph, and so we just calculate their areas using the end of the array as the right bound.

In the example above, bars with height 1, 2 and 3 would remain on the stack after the iteration through the array.

def largestRectangleArea(self, heights: List[int]) -> int:
	ans = 0
	stack = [] # (index, height)
	
	for i, h in enumerate(heights):
		# if previous height on stack is bigger
		# it can't be extended anymore
		prev_i = None
		while len(stack) and stack[-1][1] > h:
			prev_i, prev_height = stack.pop()
			ans = max(ans, (i-prev_i) * prev_height)
		
		# if we popped some elements off, this new
		# bar can essentially be extended "back" through
		# all the bars that we popped off
		if prev_i is not None:
			stack.append((prev_i, h))
		else:
			stack.append((i, h))
	
	# deal with bars that managed to extend
	# to the end of the histogram
	n = len(heights)
	for i, h in stack:
		ans = max(ans, (n-i)*h)
	
	return ans

neetcode video walkthrough

• 00:20 problem explanation.
• 01:01 optimization intuition, we can’t extend a square to the right if the next bar is shorter.
• 01:42 we have to take the shortest bar for our rectangle height.
• 02:44 if the heights are in increasing order, we can always extend a square to the right!
• 02:55 monotonic stack intuition and walkthrough.
• 04:35 one more example.
• 05:50 algorithm explanation and walkthrough.
• 07:39 tricky indexing.
  • when we pop off bars, we have to consider that this shorter bar could’ve also been extended left through the popped bars.
• 08:49 we’re always considering the square that starts from the index we’re popping.
• 11:05 elements that are left in the stack were able to be extended to the end of the histogram, compute the area accordingly.
• 14:03 writing the code.