72. edit distance

Given two strings word1 and word2, return the minimum number of operations required to convert word1 to word2.

You have the following three operations permitted on a word:

• Insert a character
• Delete a character
• Replace a character

solutions

recursion with memoization

We maintain two pointers, one on each string. At any point in time, there are two scenarios:

1. The two characters we are looking at match, and so no edit is required. We move onto the next pair of characters.
2. The two characters don’t match. We can either replace one character to match the other, delete one of them, or insert one to match the other.

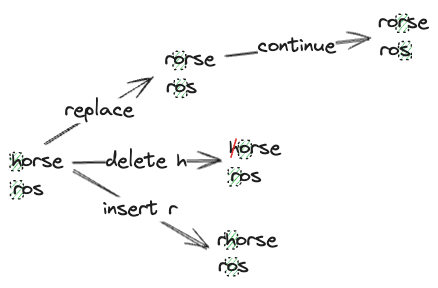
See the diagram for a visualization:

def minDistance(self, word1: str, word2: str) -> int:
	# always make s1 the longer string
	if len(word2) > len(word1):
		word1, word2 = word2, word1
	
	memo = {}
	
	def recurse(p1, p2):
		"""
		we've reached the end of one/both of the words
		any remaining characters in the other word
		can be inserted/deleted
		"""
		# base case
		if p1 == len(word1) or p2 == len(word2):
			if p1 == len(word1):
				return len(word2) - p2
			else:
				return len(word1) - p1
		  
		if (p1, p2) in memo:
			return memo[(p1, p2)]
		
		# if chars are the same, no edit necessary
		if word1[p1] == word2[p2]:
			memo[(p1, p2)] = recurse(p1+1, p2+1)
			return memo[(p1, p2)]
 
		memo[(p1, p2)] = min(
			recurse(p1+1, p2+1), # replace
			recurse(p1+1, p2), # delete
			recurse(p1, p2+1) # insert
		)+1
      return memo[(p1, p2)]
	
	return recurse(0, 0)

2d dynamic programming

We essentially reproduce the solution above, but use a 2d array instead of recursion with a cache.

Note that we go top-down (reverse iterate through the array), to mimic the behavior that the recursive method uses. This is useful when trying to directly convert solutions from recursion to DP (instead of having to reason about a bottom-up approach).

def minDistance(self, word1: str, word2: str) -> int:
	dp = [[1000] * (len(word2) + 1) for i in range(len(word1) + 1)]
	
	# base cases for when we reach the end of
	# the shorter string
	for j in range(len(word2) + 1):
		dp[len(word1)][j] = len(word2) - j
	for i in range(len(word1) + 1):
		dp[i][len(word2)] = len(word1) - i
	  
	for i in range(len(word1) - 1, -1, -1):
		for j in range(len(word2) - 1, -1, -1):
			if word1[i] == word2[j]:
				dp[i][j] = dp[i + 1][j + 1]
			else:
				dp[i][j] = 1 + min(dp[i + 1][j], dp[i][j + 1], dp[i + 1][j + 1])
	return dp[0][0]