695. max area of island

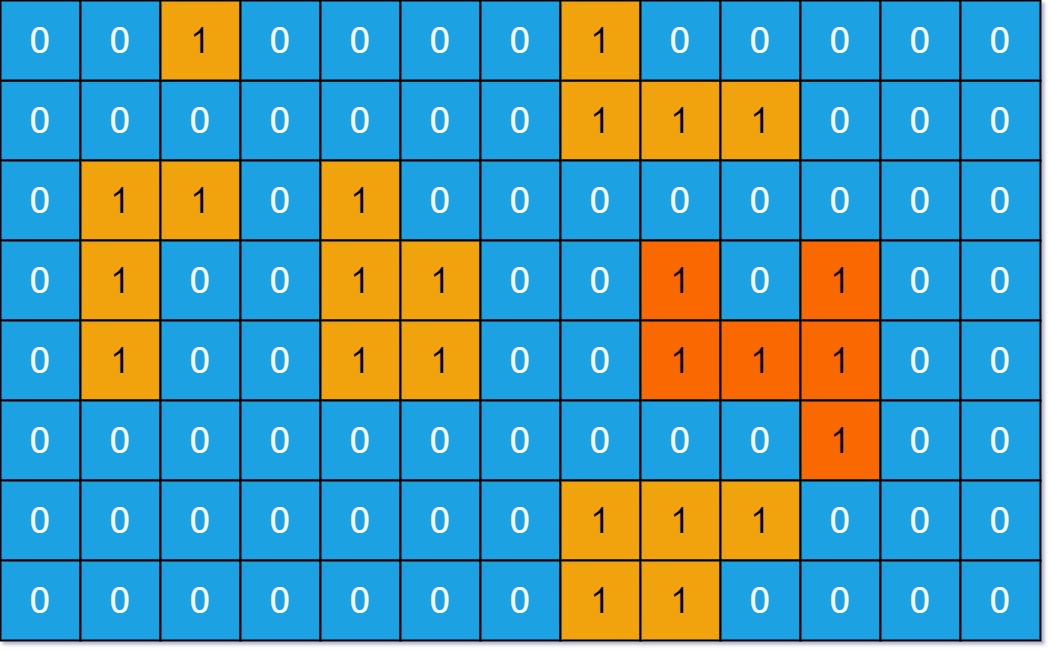
You are given an m x n binary matrix grid. An island is a group of 1’s (representing land) connected 4-directionally (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.

The area of an island is the number of cells with a value 1 in the island.

Return the maximum area of an island in grid. If there is no island, return 0.

solutions

dfs w/ sinking

• we just do a dfs on the areas that have a 1, sink islands that we already visit, and keep track of the biggest island.

def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
	ans = 0
	dirs = [[0, 1], [1, 0], [0, -1], [-1, 0]]
	
	def dfs(i, j):
		if grid[i][j] == 0:
			return 0
 
		# sink
		grid[i][j] = 0
	
		# recurse on neighbors 
		rest = 0
		for d in dirs:
			ni, nj = i + d[0], j + d[1]
			if 0 <= ni < len(grid) and 0 <= nj < len(grid[0])
				rest += dfs(ni, nj)
		return 1 + rest
	
	for i in range(len(grid)):
		for j in range(len(grid[0])):
			if grid[i][j] == 1:
				ans = max(ans, dfs(i, j))
	return ans

union-find

Definitely overkill, but we can iterate through every square, and union with the upper and left surrounding squares if they are equal to 1 (we only do those because we are guaranteed to have already created those components in our UF).

class UnionFind:
	def __init__(self):
		self.parents = {}
		self.sizes = {}
 
	def find(self, u):
		if u != self.parents[u]:
			self.parents[u] = self.find(self.parents[u])
		return self.parents[u]
 
def union(self, u, v):
pu, pv = self.find(u), self.find(v)
  
if pu == pv:
return -1
if self.sizes[pu] < self.sizes[pv]:
pu, pv = pv, pu
self.parents[pv] = pu
self.sizes[pu] += self.sizes[pv]
return self.sizes[pu]
  
class Solution:
def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
uf = UnionFind()
res = 0
  
for i in range(len(grid)):
for j in range(len(grid[0])):
if grid[i][j] == 1:
# create the node
uf.parents[(i, j)] = (i, j)
uf.sizes[(i, j)] = 1
res = max(res, 1)
  
# union upper
if i > 0 and grid[i-1][j] == 1:
res = max(res, uf.union((i, j), (i-1, j)))
# union
if j > 0 and grid[i][j-1] == 1:
res = max(res, uf.union((i, j), (i, j-1)))
return res