490. the maze

There is a ball in a maze with empty spaces (represented as 0) and walls (represented as 1). The ball can go through the empty spaces by rolling up, down, left or right, but it won’t stop rolling until hitting a wall. When the ball stops, it could choose the next direction.

Given the m x n maze, the ball’s start position and the destination, where start = [startrow, startcol] and destination = [destinationrow, destinationcol], return true if the ball can stop at the destination, otherwise return false.

You may assume that the borders of the maze are all walls (see examples).

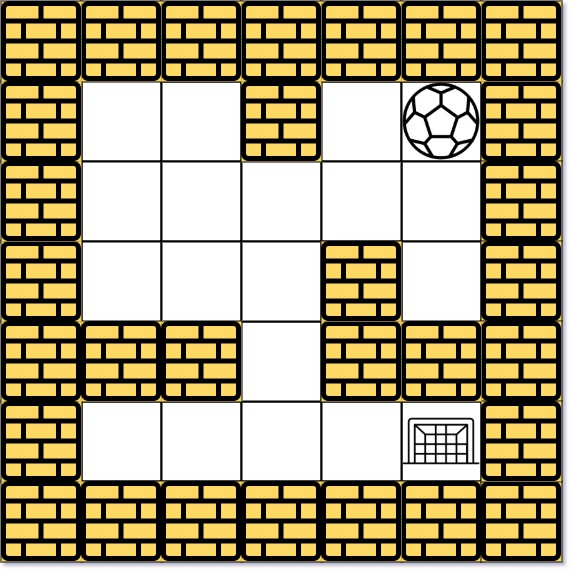
solution

Pretty basic DFS solution, but instead of just looking in 4 directions, we have to simulate the rolling until it stops.

We can keep a seen set to make sure DFS doesn’t infinitely loop, and use memo to memoize the recursive calls.

def hasPath(self, maze: List[List[int]], start: List[int], destination: List[int]) -> bool:
	m, n = len(maze), len(maze[0])
	dirs = [[0,1],[1,0],[0,-1],[-1,0]]
	seen = set([tuple(start)])
	memo = {}
	  
	def dfs(x, y):
		if (x, y) in memo:
			return memo[(x, y)]
 
		if x == destination[0] and y == destination[1]:
			return True
 
		# simulate rolling in all
		# four directions until stop
		can_reach_end = False
		  
		for dx, dy in dirs:
			cx, cy = x, y
			nx, ny = cx+dx, cy+dy
			while 0 <= nx < m and 0 <= ny < n and maze[nx][ny] == 0:
				cx, cy = nx, ny
				nx, ny = nx+dx, ny+dy
		  
			# stopped rolling
			if (cx, cy) not in seen:
				seen.add((cx, cy))
				can_reach_end = can_reach_end or dfs(cx, cy)
				seen.remove((cx, cy))
 
		memo[(x, y)] = can_reach_end
		return can_reach_end
	
	return dfs(start[0], start[1])