45. jump game ii

You are given a 0-indexed array of integers nums of length n. You are initially positioned at nums[0].

Each element nums[i] represents the maximum length of a forward jump from index i. In other words, if you are at nums[i], you can jump to any nums[i + j] where:

• 0 <= j <= nums[i] and
• i + j < n

Return the minimum number of jumps to reach nums[n - 1]. The test cases are generated such that you can reach nums[n - 1].

dynamic programming

class Solution:
    def jump(self, nums: List[int]) -> int:
        dp = [float("inf")]*len(nums)
        dp[-1] = 0
 
        for i in reversed(range(len(nums)-1)):
            for jump in range(i+1, min(len(nums), i+nums[i]+1)):
                if dp[jump] is not None:
                    dp[i] = min(dp[i], dp[jump]+1)
        return dp[0]

• we just keep track of the minimum number of jumps is required to reach the end from index $i$ in dp[i].
  • our base case is 0 in the final index of the dp array.
• $O(n^2)$ time complexity, $O(n)$ space complexity.

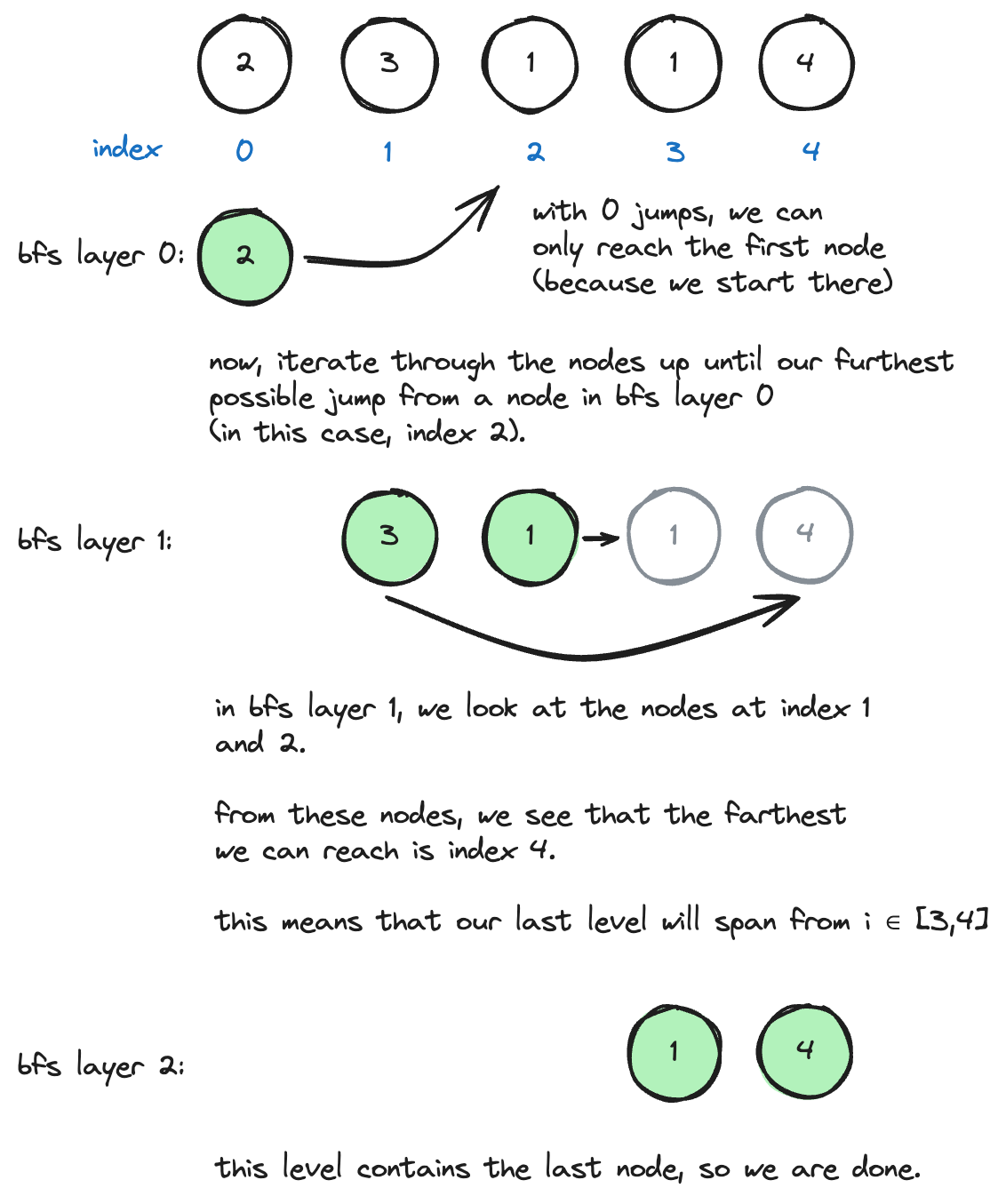
level-order bfs

class Solution:
	def jump(self, nums: List[int]) -> int:
		n = len(nums)
		furthest = 0
		last_jumped = 0
		jumps = 0
 
		i = 0
 
		while last_jumped < n-1:
			furthest = max(furthest, i + nums[i])
			if i == last_jumped:
				jumps += 1
				last_jumped = furthest
			i += 1
		return jumps

• instead of doing dynamic programming, we can instead notice that this problem can be solved as a “shortest path” bfs problem.
• it’s important to note that this solution improves upon the previous solution, to $O(n)$ time, because we don’t do any of the repeated work of iterating through all of the possible jumps from each step.
  • instead, we just find the farthest possible step that we can reach from each bfs level, which is $O(1)$ time per step.