Given the root of a binary tree and an integer targetSum, return the number of paths where the sum of the values along the path equals targetSum.
The path does not need to start or end at the root or a leaf, but it must go downwards (i.e., traveling only from parent nodes to child nodes).
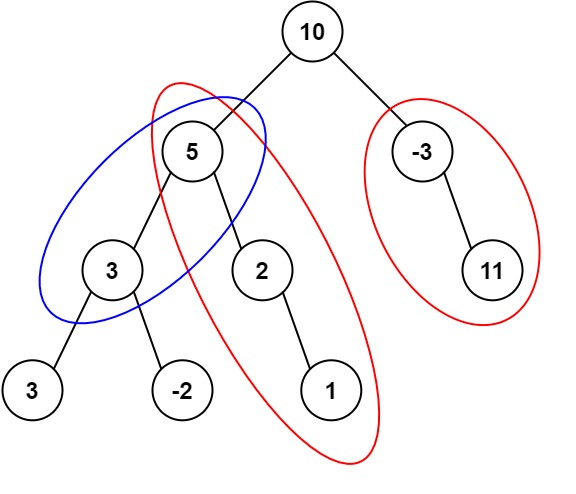
solutions
nested recursion starting from every node
Each call of recurse finds all the paths starting at node. In the main function, we try calling recurse with every node.
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> int:
if not root:
return 0
ans = 0
acc = 0
def recurse(node):
nonlocal acc, ans
if not node:
return
acc += node.val
if acc == targetSum:
ans += 1
recurse(node.left)
recurse(node.right)
# backtrack
acc -= node.val
# all paths starting at root
recurse(root)
# all paths starting at children
ans += self.pathSum(root.left, targetSum)
ans += self.pathSum(root.right, targetSum)
return ans recursion + prefix sums
We basically do the idea of 523-continuous-subarray-sum or 525-contiguous-array. We keep a count of the number of times each prefix appears, and then we can calculate how many paths ending at the current node sum to targetSum in constant time.
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> int:
ans = 0
prefix_counts = Counter()
prefix_counts[0] = 1
acc = 0
def recurse(node):
nonlocal acc, ans
if not node:
return
acc += node.val
ans += prefix_counts[acc-targetSum]
prefix_counts[acc] += 1
recurse(node.left)
recurse(node.right)
# backtrack
prefix_counts[acc] -= 1
acc -= node.val
recurse(root)
return ans