386. lexicographical numbers

Given an integer n, return all the numbers in the range [1, n] sorted in lexicographical order.

You must write an algorithm that runs in O(n) time and uses O(1) extra space.

solutions

The main intuition is to realize that lexicogaphical ordering relies on checking ordering per digit. So, we can model every possible number as a tree:

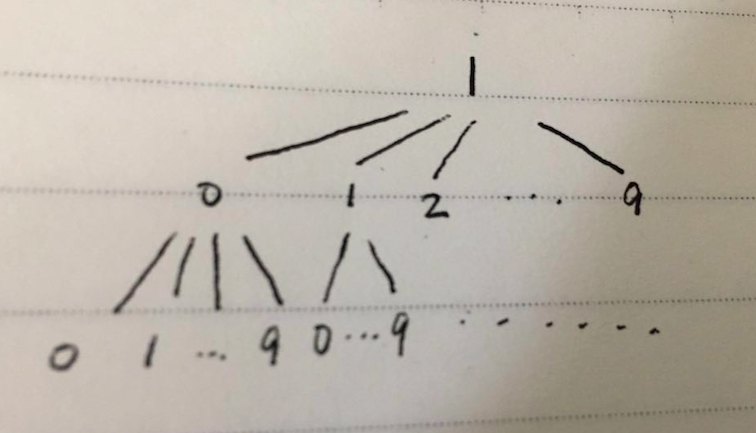
recursive dfs

# O(n)
def lexicalOrder(self, n: int) -> List[int]:
	res = []
	def dfs(val):
		if val > n:
			return
 
		res.append(val)
	  
		for i in range(10):
			dfs(val*10+i)
 
	for i in range(1, 10):
		dfs(i)
	return res

iterative

We can perform the same pattern as DFS would do, but fully iteratively. There’s three scenarios:

1. If we can go a level deeper in the tree (val * 10 <= n), then we should.
2. If we can continue on the current level (val + 1 <= n), then we should. Note that if this causes us to reach a new tens place value (i.e. 19 → 20), we need to remove any trailing zeroes (because 2 comes before 20).
3. If we’re strictly at a value that can’t be added to (val == n), we backtrack (val //= 10) and then increment the previous level’s value by one. Note that once again, we need to remove trailing zeroes if this leads to a tens place change.

# O(n), O(1) space
def lexicalOrder(self, n: int) -> List[int]:
	res = []
	val = 1
	  
	for i in range(n):
		res.append(val)
	  
		# depth first... go as deep as possible
		if val * 10 <= n:
			val *= 10
		# if we can't go down a level
		# but can add one, add it and
		# remove any trailing zeroes
		elif val + 1 <= n:
			val += 1
			while val % 10 == 0:
				val //= 10
		# else, we need to backtrack
		# and advance the previous spot's value
		else:
			val //= 10
			# if this increment causes the tens place
			# to change, we need to remove trailing zeroes
			val += 1
			while val % 10 == 0:
				val //= 10
	  
	return res