2863. maximum length of semi-decreasing subarrays

You are given an integer array nums.

Return the length of the longest semi-decreasing subarray of nums, and 0 if there are no such subarrays.

• A subarray is a contiguous non-empty sequence of elements within an array.
• A non-empty array is semi-decreasing if its first element is strictly greater than its last element.

solutions

In terms of general intuition, we can distill down the definition of a semi-decreasing subarray to any pair of values, $n_i$ and $n_j$ such that $i<j$ and $n_i>n_j$.

Furthermore, assuming that $n_i$ and $n_j$ are the two values for the longest semi-decreasing subarray in an array $A$, we need the following to hold.

1. There doesn’t exist any $j\prime >j$ where $n_{j\prime }\le n_j$ (If this were the case, then the pair of $n_i$ and $n_{j\prime }$ would form a longer semi-decreasing subarray).
2. Likewise on the left side, there doesn’t exist any $i\prime <i$ where $n_{i\prime }\ge n_i$, as that would mean the pair of $n_{i\prime }$ and $n_j$ would form a longer semi-decreasing subarray.

sorting

The first solution I came up with was to sort the array (while maintaining indices), as this would allow me to iterate through the numbers in purely non-increasing order, meaning that any time I saw a number at index $j$, I know that any indices I’ve already passed could be used as the $i$ to form a valid pair.

Initially, I did this by maintaining a min_idx_seen, which was used as my $i$, and then any new index seen was tested as $j$, updating ans to be the maximum pair seen.

However, this had one issue, as duplicates would be used as pairs, when they aren’t valid. To solve this, I used a sorted list to store indices, also storing the value at the index. Then, for duplicates, I would find the next smallest index that wasn’t a duplicate, if a duplicate was detected.

from sortedcontainers import SortedList
 
def maxSubarrayLength(self, nums: List[int]) -> int:
 nums_ind = [(nums[i], i) for i in range(len(nums))]
 nums_ind.sort(key=lambda x: -x[0])
 
 ans = 0
 min_indices = SortedList()
 for num, index in nums_ind:
	min_valid_idx = 1e9
	duplicate = False
	for min_idx, val in min_indices:
	  if val == num:
		 duplicate = True
	  if val > num:
		 min_valid_idx = min_idx
		 break
 
	ans = max(ans, index-min_valid_idx+1)
 
	if not duplicate:
	  min_indices.add((index, num))
 
 return ans

monotonic stack (two-pass)

This solution is absolutely not something I would have come up with myself, but I’ll try to explain the intuition.

First of all, let’s take a look at this example array, visualized as bars of varying heights.

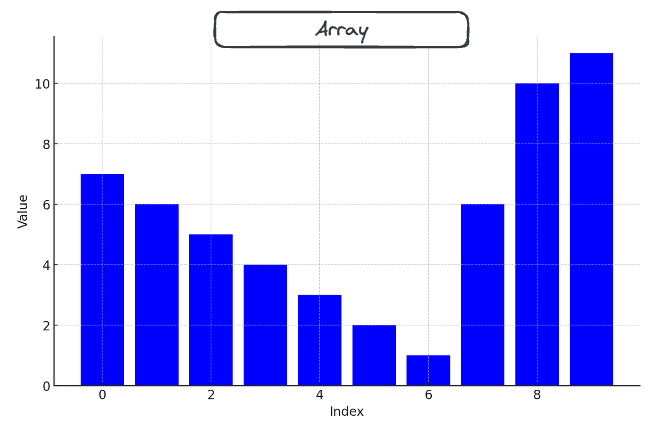
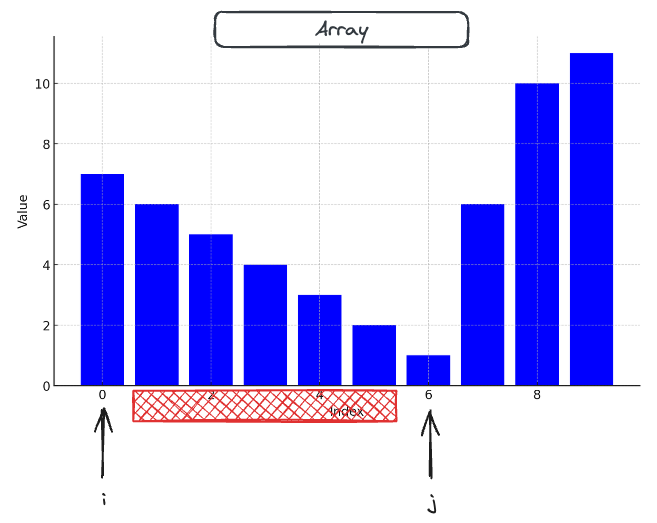
Now, the first consideration is that if we pick $j=6$, we can see that our best choice for $i$ is 0. The other thing we notice is that all the values of $i$ between 1 and 5 form valid pairs, but we don’t care about them, because the value at $i=0$ is bigger.

Furthermore, if hypothetically, there was a bar with height -1000 later on in the array at $j\prime$, we don’t care about any of the bars highlighted in red, because we would pair $j\prime$ with $i=0$.

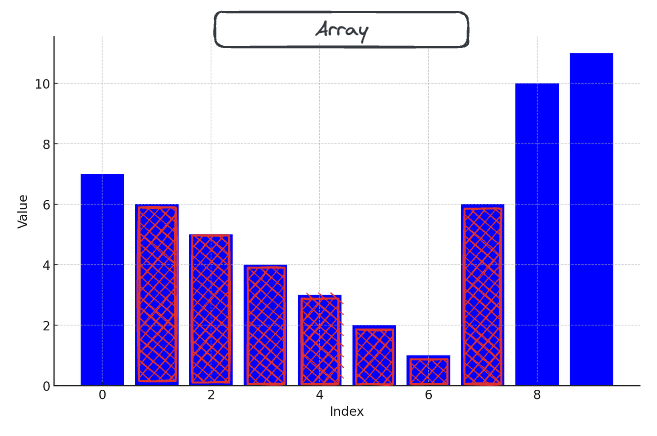
This leads to the intuition that perhaps we should create a monotonically increasing stack of numbers.

These are the numbers that remain after creating a monotonic stack.

Now, we can see that for any value $j$ that we can pick, we can find the smallest value $i$ in our monotonic stack (to the left of $j$) such that $n_i>n_j$. Because the stack is sorted, we can do this in $O(\log n)$ time.

The final breakthrough is that instead of searching through the monotonic stack for each value of $j$, we can instead iterate backwards through our array, and gradually eliminate values from the stack.

Let’s add a couple more numbers to the stack for demonstration.

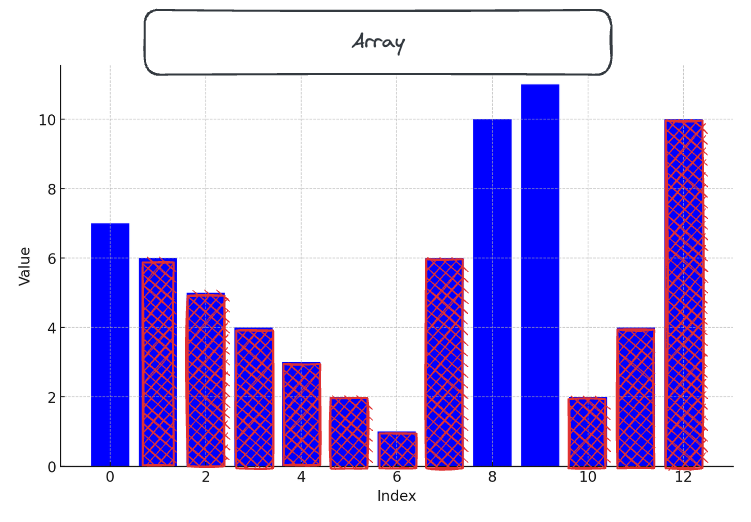
Now let’s start at $j=12$. Looking back through the monotonic stack, we see that the value at $i=9$ is larger than the value at $j$, so it is a valid pair.

We try to improve our answer, looking at $i=8$. These heights are the same, so we stop looking (as every value further left is smaller).

Now, just like the intuition above that allowed us to create the monotonic stack, we realize that because the value at $i=9$ created a valid pair with $j=12$, we don’t need to consider it for any other smaller values of $j$!

def maxSubarrayLength(self, nums: List[int]) -> int:
	stack = []
	n = len(nums)
	
	# create monotonically increasing stack
	stack = []
	for i, x in enumerate(nums):
		if not stack or stack[-1][1] < x:
			stack.append((i, x))
 
	ans = 0
	for j in reversed(range(n)):
		while stack and stack[-1][1] > nums[j]:
			i, val = stack.pop()
			ans = max(ans, j-i+1)
 
	return ans