2444. count subarrays with fixed bounds

You are given an integer array nums and two integers minK and maxK.

A fixed-bound subarray of nums is a subarray that satisfies the following conditions:

• The minimum value in the subarray is equal to minK.
• The maximum value in the subarray is equal to maxK.

Return the number of fixed-bound subarrays.

A subarray is a contiguous part of an array.

solutions

brute force

We can enumerate every possible subarray and check the minimum and maximum in the subarrays.

def countSubarrays(self, nums: List[int], minK: int, maxK: int) -> int:
	n = len(nums)
	count = 0
	  
	for i in range(n):
		for j in range(i, n):
			minv, maxv = inf, -inf
			for k in range(i, j+1):
				minv = min(minv, nums[k])
				maxv = max(maxv, nums[k])
			if minv == minK and maxv == maxK:
				count += 1
	return count

optimization #1

This solution is still enumerating every subarray, but instead of iterating over each subarray in $O(n)$, we instead strategically look at every growing subarray with left bound $i$.

If we ever see a value outside of the valid range, we can stop looking.

Else, if we ever confirm that minK and maxK exist in the subarray, we know that all extended subarrays from $i$ will also be valid, as long as we don’t see an out-of-bounds value.

def countSubarrays(self, nums: List[int], minK: int, maxK: int) -> int:
	n = len(nums)
	count = 0
	  
	for i in range(n):
		min_found = max_found = False
		for j in range(i, n):
			if nums[j] < minK or nums[j] > maxK:
				break
			if nums[j] == minK:
				min_found = True
			if nums[j] == maxK:
				max_found = True
			if min_found and max_found:
				count += 1
	return count

optimized - three pointers

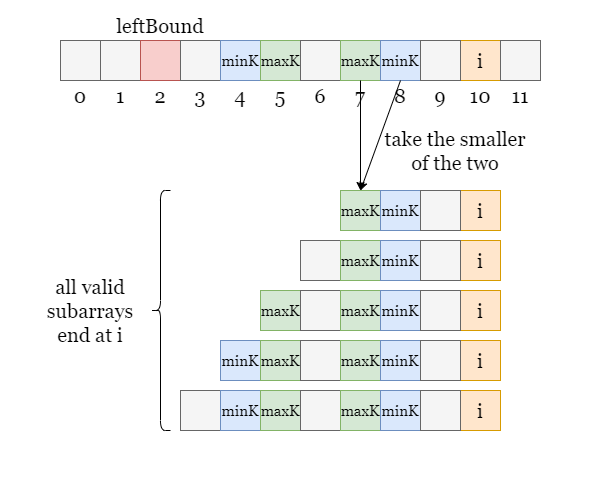
The intuition here is a little funky. At the root of it, for these problems where we are looking for “how many subarrays satisfy $X$”, a trick to avoid overcounting is to consider how many subarrays that end at index $i$ satisfy some condition.

We then have to figure out some invariant when constraining the problem to “arrays that end at $i$”.

For this problem, the constraints are as follows:

1. Both minK and maxK have to exist in the subarray, to the left.
2. No values that are out-of-bounds can exist between minK and i or maxK and i.

So, this leads us to realize that we need to keep three pointers - the leftmost occurrence of minK and maxK, as well as the rightmost occurrence of an out-of-bounds value.

Then, for subarrays ending at index $i$, we know that we can enumerate the left bound of the subarray to be any index between the previous oob value (non-inclusive) and the leftmost value out of minK and maxK.

def countSubarrays(self, nums: List[int], minK: int, maxK: int) -> int:
	n = len(nums)
	count = 0
	  
	min_pos = max_pos = oob = -1
	  
	for i in range(n):
		if nums[i] == minK:
			min_pos = i
		if nums[i] == maxK:
			max_pos = i
		if nums[i] < minK or nums[i] > maxK:
			oob = i
			min_pos = max_pos = -1
		if min_pos > -1 and max_pos > -1:
			count += min(min_pos, max_pos) - oob
	return count