221. maximal square

Given an m x n binary matrix filled with 0’s and 1’s, find the largest square containing only 1’s and return its area.

solution

class Solution:
    def maximalSquare(self, matrix: List[List[str]]) -> int:
        """
        - dp is a matrix with the same dimensions as matrix
        - dp[i][j] stores the side length of the biggest one square anchored bottom-right at matrix[i][j]
        - iterate from top-left, going right, then down
        - at each index, check the min square anchored at (i, j-1), (i-1, j), and (i-1, j-1)
        - return max(dp)
        """
 
        dp = [[0]*len(matrix[0]) for row in matrix]
        best = 0
        # base case bottom row and right column
        for i in range(len(matrix[0])):
            dp[0][i] = int(matrix[0][i])
            best = max(best, dp[0][i])
        
        for i in range(1, len(matrix)):
            for j in range(len(matrix[i])):
                if matrix[i][j] == "0":
                    dp[i][j] = 0
                elif j == 0:
                    dp[i][j] = int(matrix[i][j])
                else:
                    dp[i][j] = min(
                        dp[i][j-1], dp[i-1][j], dp[i-1][j-1]
                    ) + 1
                best = max(best, dp[i][j])
        return best ** 2

• pretty cool geometry and dynamic-programming problem.
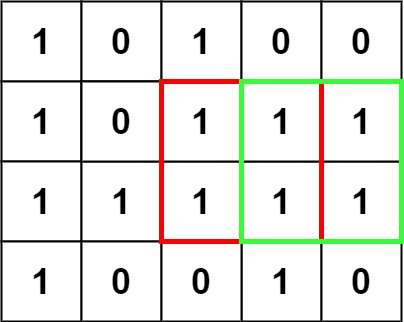
• we can figure out the maximum sized square anchored at the top corner of some index by looking at the biggest squares that are anchored at the other three quadrants.

  221-e1.excalidraw

  ⚠ Switch to EXCALIDRAW VIEW in the MORE OPTIONS menu of this document. ⚠

  Text Elements

  length = 1

  Link to original

• in this example, we see that given the three squares of side length 2, 3, and 4 from the top-right, bottom-left, and bottom-right quadrants, we are able to create a square of side length $2+1=3$ from our top-left corner.

slight optimization

class Solution:
    def maximalSquare(self, matrix: List[List[str]]) -> int:
        """
        - dp is a matrix with the same dimensions as matrix
        - dp[i][j] stores the side length of the biggest one square anchored bottom-right at matrix[i][j]
        - iterate from top-left, going right, then down
        - at each index, check the min square anchored at (i, j-1), (i-1, j), and (i-1, j-1)
        - return max(dp)
        """
 
        prev = [int(x) for x in matrix[0]]
        best = max(prev)
        
        for i in range(1, len(matrix)):
            next_row = [int(x) for x in matrix[i]]
            for j in range(len(matrix[i])):
                if matrix[i][j] == "0":
                    next_row[j] = 0
                elif j == 0:
                    next_row[j] = int(matrix[i][j])
                else:
                    next_row[j] = min(
                        next_row[j-1], prev[j], prev[j-1]
                    ) + 1
                best = max(best, next_row[j])
            prev = next_row
        return best ** 2

• we only ever need to read the values from the previous row of the dp array, so we can optimize for space by just keeping track of the current and previous rows.