116. populating next right pointers in each node

You are given a perfect binary tree where all leaves are on the same level, and every parent has two children. The binary tree has the following definition:

solutions

level-order traversal

This is the logical/simple way to do this. Just do level-order traversal, and then for each level, link adjacent nodes.

def connect(self, root: 'Optional[Node]') -> 'Optional[Node]':
	if not root:
		return root
	  
	q = deque([root])
	  
	def link_level():
		i = 0
		while i+1 < len(q):
			q[i].next = q[i+1]
			i += 1
	  
	while q:
		level_len = len(q)
	  
		for _ in range(level_len):
			cur = q.popleft()
	  
			if cur.left:
				q.append(cur.left)
			if cur.right:
				q.append(cur.right)
			link_level()
 
	return root

iterative O(1)

Instead of keeping track of the whole level in a queue, we just treat each level as a sort of linked list, and link up a whole level before moving onto the next level.

There are two connections to consider:

1. Linking a node’s left child to it’s right child (trivial).
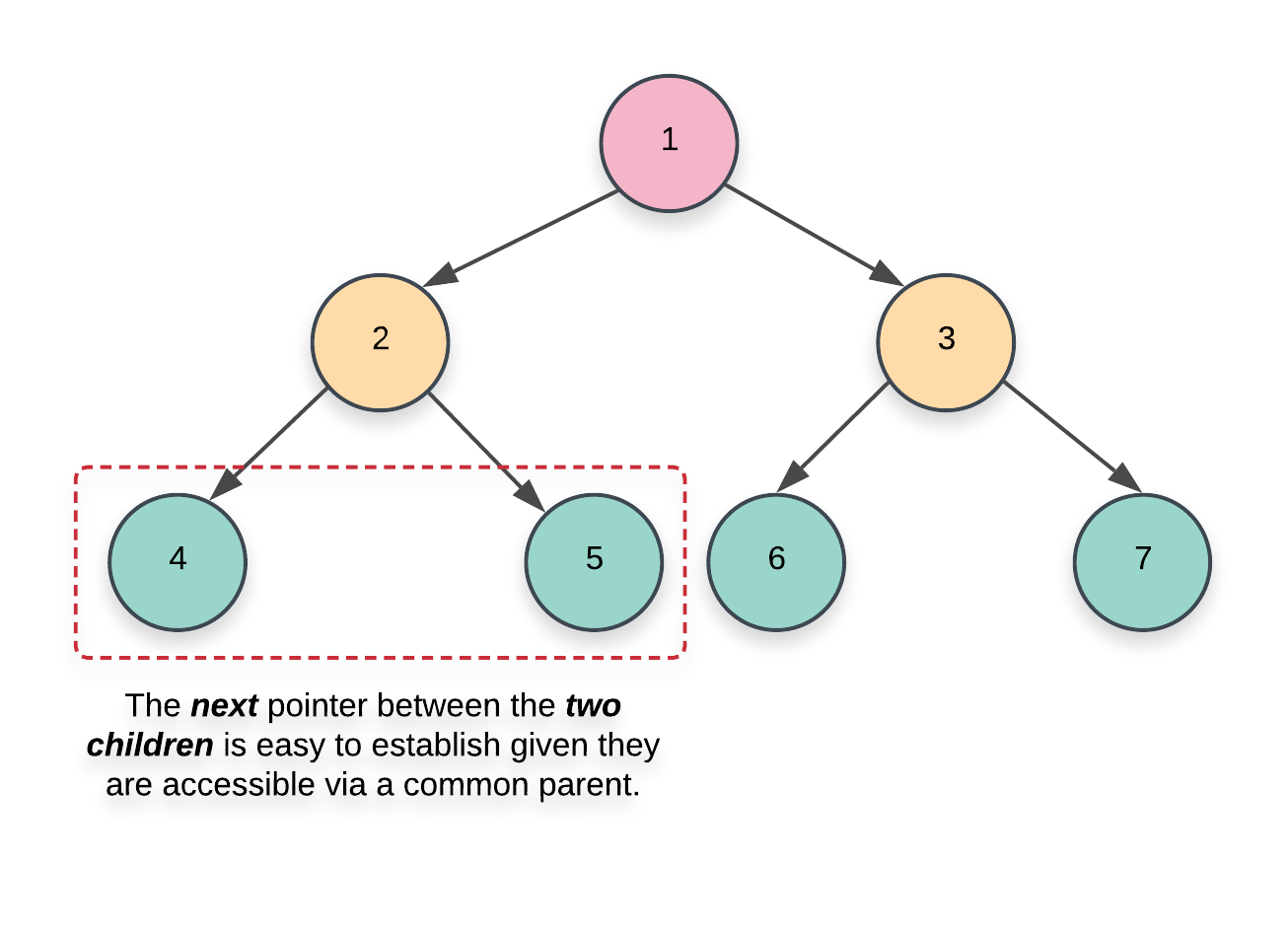
2. Linking a node’s right child to node.next’s left child. Note that in this case, we just need to do node.right = node.next.left. If we can guarantee that all the next pointers are set, this can be done safely.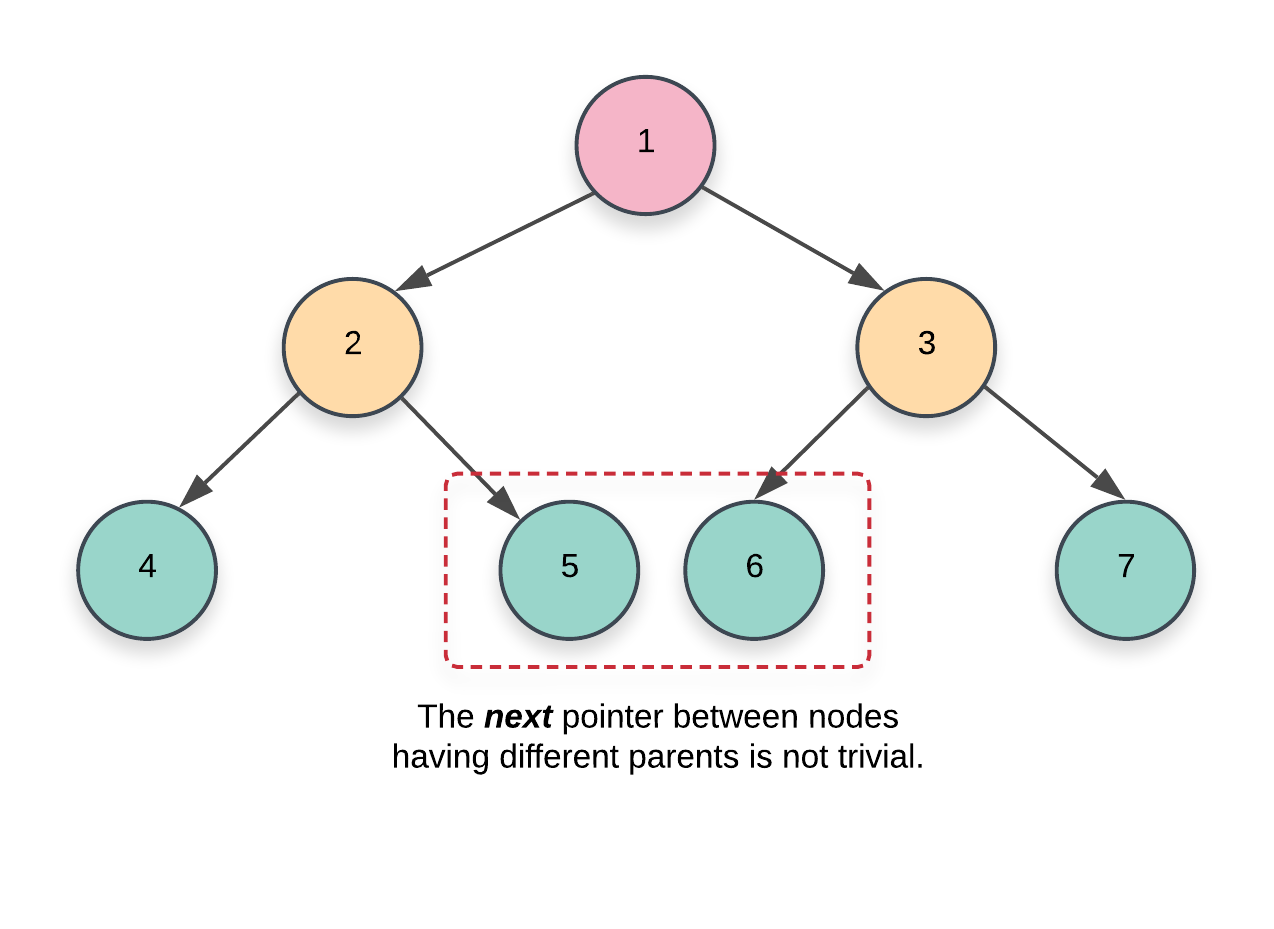

So, we maintain a reference to the “head” of the current level, and traverse left to right, setting these two types of connections. Once we’re done, we can update leftmost and move onto the next level.

We only move on to the level $N+1$ when we are done establishing the next pointers for the level $N$. Since we have access to all the nodes on a particular level via the next pointers, we can use these next pointers to establish the connections for the next level or the level containing their children.

def connect(self, root: "Node") -> "Node":
 
	if not root:
		return root
	
	# Start with the root node. There are no next pointers
	# that need to be set up on the first level
	leftmost = root
	
	# Once we reach the final level, we are done
	# leftmost.left will be None once we reach leaves
	while leftmost.left:
	
		# Iterate the "linked list" starting from the head
		# node and using the next pointers, establish the
		# corresponding links for the next level
		head = leftmost
		while head:
	
			# CONNECTION 1
			head.left.next = head.right
	
			# CONNECTION 2
			if head.next:
				head.right.next = head.next.left
	
			# Progress along the list (nodes on the current level)
			head = head.next
	
		# Move onto the next level
		leftmost = leftmost.left
	
	return root

recursion

The problem follow-up asks for a constant space solution.

W can recursively populate the next pointers of the current node’s children.

class Solution:
    def connect(self, root: 'Optional[Node]') -> 'Optional[Node]':
        if root:
            if root.right:
                if root.next:
                    root.right.next = root.next.left
                self.connect(root.right)
            
            if root.left:
                root.left.next = root.right
                self.connect(root.left)
        
        return root