865. smallest subtree with all the deepest nodes

Given the root of a binary tree, the depth of each node is the shortest distance to the root.

Return the smallest subtree such that it contains all the deepest nodes in the original tree.

A node is called the deepest if it has the largest depth possible among any node in the entire tree.

The subtree of a node is a tree consisting of that node, plus the set of all descendants of that node.

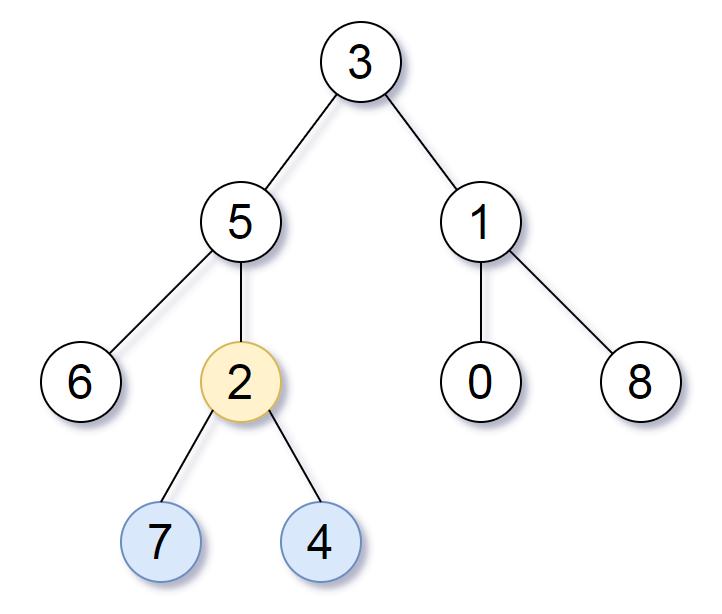
solution

We first find the maximum depth of the tree. Once we do this, this question becomes very similar to 236-lowest-common-ancestor-of-a-binary-tree. We do a postorder traversal, and realize that if both the left and right subtrees have a maximum depth equal to max_depth, we should set res to it.

Because we’re doing a postorder traversal, the last node we traverse that satisfies this condition is the one that is the highest up node that contains subtrees with all the deepest nodes.

def findMaxDepth(self, node):
	if not node: return 0
	return 1 + max(
		self.findMaxDepth(node.left),
		self.findMaxDepth(node.right)
	)
  
def subtreeWithAllDeepest(self, root: TreeNode) -> TreeNode:
	res = None
	max_depth = self.findMaxDepth(root)
	  
	def dfs(node, depth):
		nonlocal res, max_depth
		"""
		if depth of node is max_depth, set res to it
		if max depth of node.left and node.right is both max_depth,
		update res
		
		postorder traversal processes parent last, so we should always update res if we see another node that contains max depth in left and right subtree
		"""
		if not node:
			return depth-1
 
		# guaranteed leaf node
		if depth == max_depth:
			res = node
			return depth
		  
		max_depth_left = dfs(node.left, depth+1)
		max_depth_right = dfs(node.right, depth+1)
		  
		if max_depth_left == max_depth_right == max_depth:
			res = node
		return max(max_depth_left, max_depth_right)
	  
	dfs(root, 1)
	return res