218. the skyline problem

A city’s skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. Given the locations and heights of all the buildings, return the skyline formed by these buildings collectively.

The geometric information of each building is given in the array buildings where buildings[i] = [lefti, righti, heighti]:

• lefti is the x coordinate of the left edge of the ith building.
• righti is the x coordinate of the right edge of the ith building.
• heighti is the height of the ith building.

You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at height 0.

The skyline should be represented as a list of “key points” sorted by their x-coordinate in the form [[x1,y1],[x2,y2],...]. Each key point is the left endpoint of some horizontal segment in the skyline except the last point in the list, which always has a y-coordinate 0 and is used to mark the skyline’s termination where the rightmost building ends. Any ground between the leftmost and rightmost buildings should be part of the skyline’s contour.

Note: There must be no consecutive horizontal lines of equal height in the output skyline. For instance, [...,[2 3],[4 5],[7 5],[11 5],[12 7],...] is not acceptable; the three lines of height 5 should be merged into one in the final output as such: [...,[2 3],[4 5],[12 7],...]

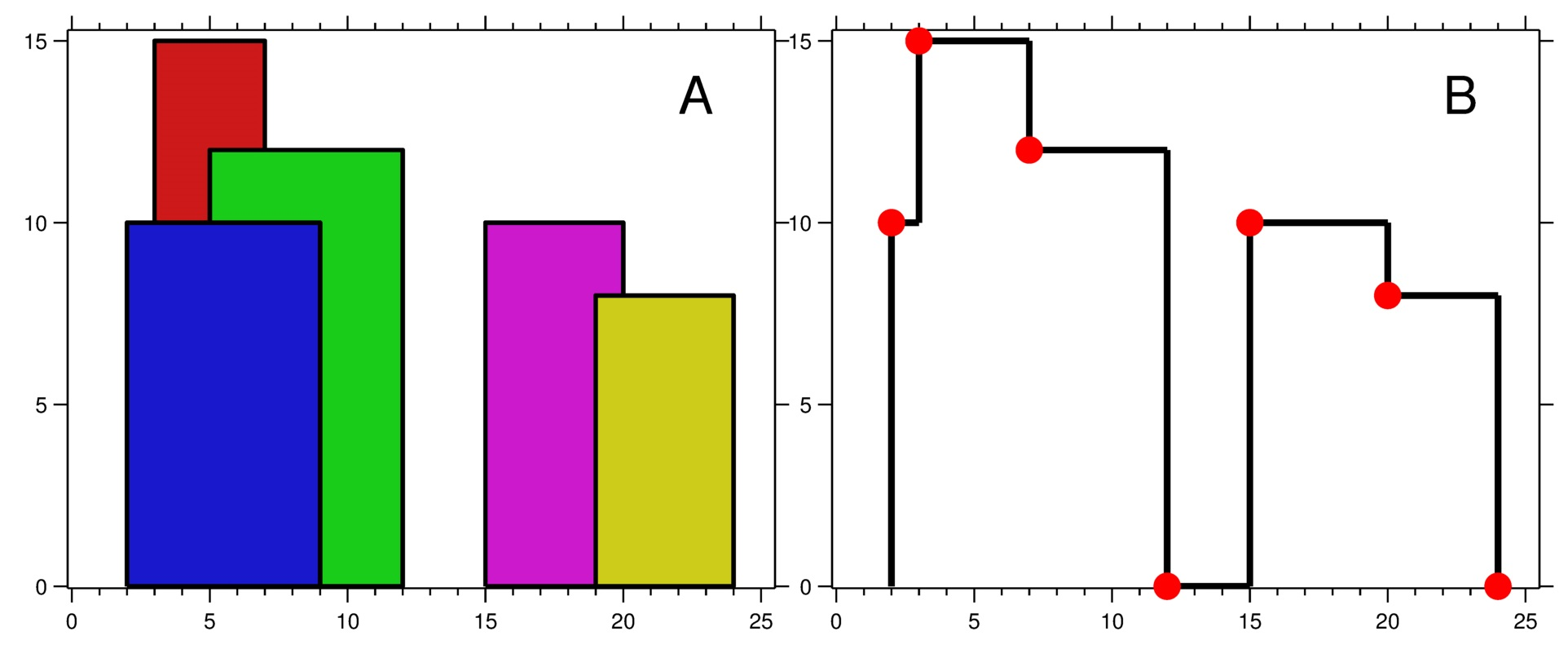
solutions

line-sweep

The primary intuition here is that the height of our skyline only changes when something changes… in this case, either when a building starts or ends.

Furthermore, every time there’s a start/end event at position $x$, our skyline updates to be the point of the highest building that covers position $x$.

So, what we can do is sort every event, both start and end, and use a max-heap to return the highest building out of the ones currently considered. Like with other heap problems, we can make use of lazy deletion to just ensure that the value at the top of the heap is a valid one.

A special note is that we have to have some secondary sorting:

1. We need to have starts come before ends in the case of equal positions, because we don’t want to count a drop + rise when we have two buildings touching and equal height.
2. We need to tertiary sort by the heights descending, in case we have multiple buildings start at the same position with different heights. We want to make sure to take the tallest building and add it to res.

def getSkyline(self, buildings: List[List[int]]) -> List[List[int]]:
	START = 0
	END = 1
	  
	# set up line-sweep
	# sorted list of all points of interest (starts and ends)
	a = []
	for start, end, height in buildings:
		a.append((start, height, START, end))
		a.append((end, height, END, start))
 
	# secondary sort by type:
	# process all starts before ends to avoid cases where
	# two buildings are touching and same height. This prevents
	# us from unnecessarily processing a drop in the skyline height
 
	# tertiary sort by height:
	# if two buildings start at the same point but have different heights,
	# we don't want to process the shorter building first and
	# have a skyline point that's lower than it should be.
	a.sort(key=lambda x: (x[0], x[2], -x[1]))
	  
	res = []
	cur_buildings = [(0, inf)]
	  
	# maintain max heap of buildings not yet passed
	# at every point of interest, update the skyline with
	# tallest building currently in the window.
	for pos, height, typ, other_pos in a:
		if typ == START:
			# store ending position in heap
			heappush(cur_buildings, (-height, other_pos))
 
		# lazy deletion
		while cur_buildings and cur_buildings[0][1] <= pos:
			heappop(cur_buildings)
 
		next_height = -cur_buildings[0][0]
		if len(res) == 0 or next_height != res[-1][1]:
			res.append([pos, next_height])
	return res