1391. check if there is a valid path in a grid

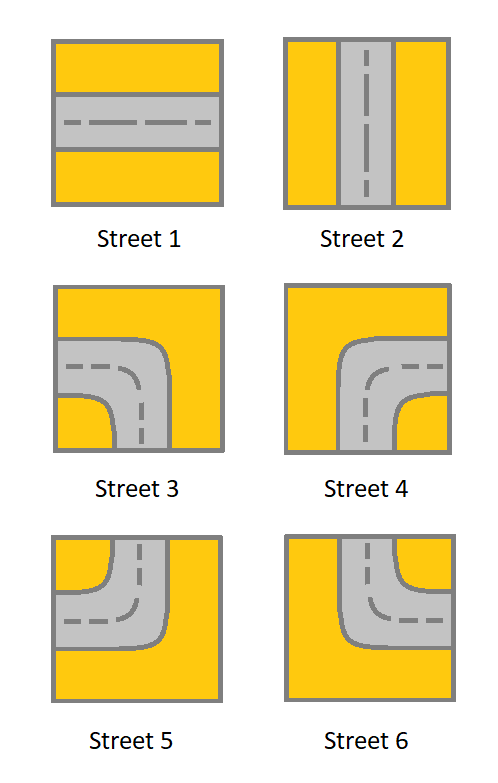
You are given an m x n grid. Each cell of grid represents a street. The street of grid[i][j] can be:

• 1 which means a street connecting the left cell and the right cell.
• 2 which means a street connecting the upper cell and the lower cell.
• 3 which means a street connecting the left cell and the lower cell.
• 4 which means a street connecting the right cell and the lower cell.
• 5 which means a street connecting the left cell and the upper cell.
• 6 which means a street connecting the right cell and the upper cell.

solution

This is basically a spin on a classic “find the path” problem, but we have an extra condition specifying which directions we can enter/leave from each cell.

Create a hashmap to represent those, and by defining dirs in a clockwise direction, we can get the “opposite” direction (e.g. if we exit from the right, we enter from the left) by doing a simple addition + modulo.

def hasValidPath(self, grid: List[List[int]]) -> bool:
	m, n = len(grid), len(grid[0])
	# up, right, down, left
	dirs = [[-1,0],[0,1],[1,0],[0,-1]]
	  
	# valid ingress/egress { grid_type: set(directions connected) }
	connections = {
		1: {1, 3},
		2: {0, 2},
		3: {2, 3},
		4: {1, 2},
		5: {0, 3},
		6: {0, 1},
	}
	  
	visited = set([(0, 0)])
	q = deque([(0, 0)])
	while q:
		x, y = q.popleft()
		  
		if (x, y) == (m-1, n-1):
			return True
		  
		# i is the egress direction
		# (i+2)%4 is the ingress direction
		for i in range(len(dirs)):
			# can't leave through this direction
			if i not in connections[grid[x][y]]:
				continue
		  
			dx, dy = dirs[i][0], dirs[i][1]
			nx, ny = x+dx, y+dy
		  
			if 0 <= nx < m and 0 <= ny < n:
				if (nx, ny) not in visited:
					ingress_dir = (i+2)%4
					if ingress_dir in connections[grid[nx][ny]]:
						visited.add((nx, ny))
						q.append((nx, ny))
 
	return False